
Bachelor's Project: DXR Fluid Simulation Rendering
-Context
This project is the practical component of my bachelor’s thesis. Its goal was to explore how to represent dynamic implicit fluids (SPH simulation) inside a real-time raytracing pipeline using the DXR API. I compared two rendering strategies: volumetric raymarching and surface reconstruction with marching cubes. Both were fully integrated into a DXR pipeline with recursive ray tracing for realistic reflection, refraction, and absorption.
The SPH simulation was originally developed by fellow Games Programming student at SAE Institute Geneva, Constantin Verine, as part of his bachelor’s project.
Click here to view his project
Together, we converted his CPU-based simulation into a compute shader, enabling me to render it using DXR ray tracing.
Raymarching
The raymarching approach directly samples the 3D density field of the SPH fluid, capturing fine volumetric details such as soft shadows, absorption, and smooth refractions. It produces visually rich results, though at a higher performance cost due to heavy sampling.
Here is a video showcasing the final result of the Raymarching approach:
Marching Cubes
The marching cubes approach reconstructs a dynamic mesh from the density field each frame. This method leverages DXR’s hardware-accelerated ray–triangle intersections, making it more efficient, but at the cost of less volumetric detail and flatter shadows.
Here is a video showcasing the final result of the Marching Cubes approach:
Rendering Comparison
The images below highlight the contrast between the two methods. Raymarching (left) delivers a smoother, more volumetric appearance with realistic refractions and shading, while Marching Cubes (right) provides sharper geometry and more stable performance, but with flatter visual detail.
| Raymarching | Marching Cubes |
|---|---|

|

|
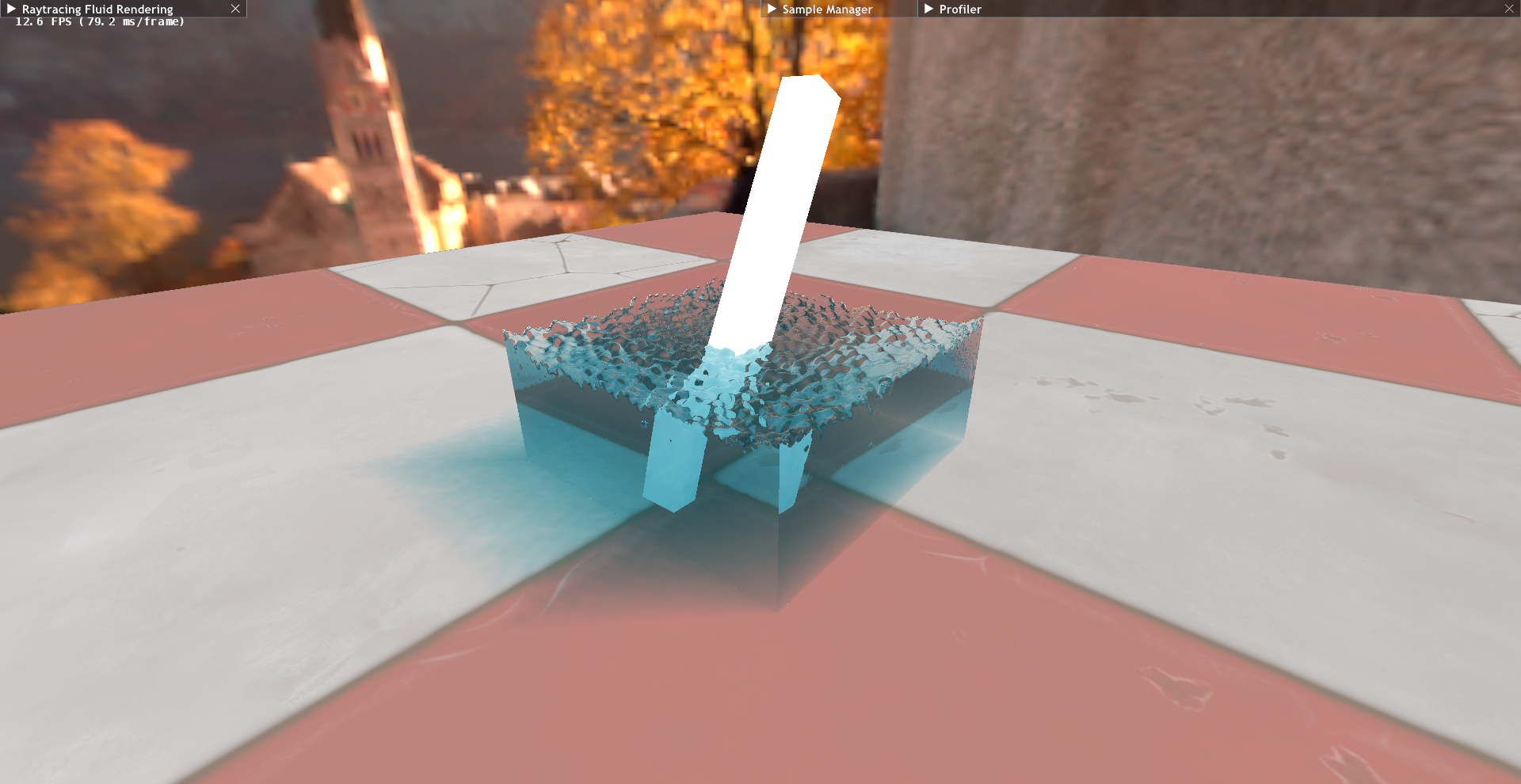
|

|
| Raymarching | Marching Cubes |
SPH Simulation
The SPH fluid simulation was originally developed by Constantin Verine as part of his bachelor’s project. Together, we adapted his CPU implementation into a GPU compute shader, enabling real-time execution within the DXR pipeline. To optimize performance, we introduced a hash grid for neighbor search and implemented an iterative bitonic sort, which efficiently reorders particles in parallel to accelerate spatial queries and interaction calculations.
Here is a video showcasing the simulation with 20’000 particles:
Performance Evaluation
As part of my bachelor’s thesis, I established a testing protocol to measure the average frame time of both algorithms at different rendering quality levels. The table below summarizes these results, offering a concise overview of how performance scales with visual fidelity for each approach.
The complete performance study can be found in the chapter 5 of my thesis document (PDF).
| Algorithm | Low Quality | Medium Quality | High Quality | Observations |
|---|---|---|---|---|
| Raymarching | ~35 ms (3 ray bounces) | ~63 ms (4 ray bounces) | ~103 ms (5 ray bounces) | Visual fidelity scales with recursion depth; cost grows with density sampling. |
| Marching Cubes | ~7 ms (low-res mesh) | ~23 ms (mid-res mesh) | ~440 ms (high-res mesh) | Fast at low/medium resolutions; high-res meshes become prohibitive (mesh update + BLAS rebuild). |
What did I learn ?
- Built a full DXR raytracing pipeline with custom shaders (intersection, any-hit).
- Implemented fluid optical effects: reflection, refraction, absorption.
- Explored two rendering approaches: Raymarching and Marching Cubes.
- Updated mesh vertices dynamically inside DXR acceleration structures.
- Ported a CPU-based SPH simulation to GPU using compute shaders.
- Optimized simulation with hash grids and a GPU bitonic sort.
- Stored and sampled simulation data in 3D textures.
- Conducted a quantitative performance analysis comparing both methods.