How I created an OpenGL 3D scene.

Hello, I recently learned the basics of graphics programming using the OpenGL API as part of a course module at SAE Insitute Geneva. I’ve managed to create a 3D scene using several techniques and functionalities, as follows:

• OBJ Model Loading
• Instancing
• Face and Frustum Culling
• Cubemap
• Deferred Shading
• Screen Space Ambient Occlusion (SSAO)
• Shadow Mapping
  • Directional Light Shadow Map
  • Point Light Shadow Cubemap
• Physically Based Rendering (PBR)
  • Image Based Lighting (IBL)
  • Directional Light
  • Point Light
• Emissive Textures Mapping
• Physically Based Bloom
• High Dynamic Range (HDR) + Tone Mapping + Gamma Correction

Here are different renderings of my scene:

The character model was created by Jeremy Leung, an excellent artist from Sae Institute.

I have structured the rendering process for my scene into several render passes, with each pass implementing several of the techniques listed above. It seems coherent to me to structure the different topics of my blog post in relation to these render passes:

• Geometry Pass
• SSAO Pass
• Shadow Mapping Pass
• PBR Pass
• Front Shading Pass
• Bloom Pass
• HDR Pass

I’m not going to go into detail about the technical implementations, but rather explain the process of my rendering pipelines. I will try to explain briefly and quite clearly each of the concepts used in the different render passes. Also note that my entire project was carried out with version 300 es of OpenGL. Having said that, let’s get into it.

Geometry Pass.

So the first render pass of my program is a geometry pass. This pass consists of drawing all the objects visible in my camera’s frustum to bring out their various geometric information. This allows heavier rendering to be deferred to a later stage in the graphics process, so that fewer light calculations need to be made, for example. But more importantly for my scene, it allows me to extract the essential geometric information for determining the occlusion factor of a fragment when calculating the screen space ambient occlusion (which would be the next pass).
Here is the geometric information I need to store per fragment:

• position
• normal

And because I do PBR, I need to store the object material property too in order to be able to calculate lighting afterward. That is why I need to store these information per fragment too:

• albedo
• metallic
• roughness
• ambient occlusion (from the material texture)
• emissive (value that I add after the lighting calculation)

G-Buffer.

All these data are stored in a frame buffer called the G-Buffer. Each piece of information is stored in the different color channels of a texture. I personally used all possible channels of a texture to have as few as possible to create. As a result, my first texture contains the position of the fragment in RGB and its metallic value in alpha. The second contains the normal in RGB and the roughness in alpha. The third contains the albedo in RGB and the ao in alpha, and the last just contains emissive in RGB.

One last important note: I’m storing the positions and normals in view-space so that I can calculate the SSAO correctly in the future, as this is done in view-space. This is why we don’t see a blue color in the position texture, because all Z positions are zero.

position in view space (RGB) + metallic (A)	normal in view space (RGB) + roughness (A)
albedo (RGB) + ambient occlusion (A)	emissive (RGB)

Instancing.

There’s nothing special about the pipeline I use to draw the meshes which appear only once in the scene. However, for the many gold spheres, my pipeline is a little different. These spheres are instantiated, which means that only one drawcall is needed to draw all the spheres. To further optimize this aspect, I pass the model matrices of my spheres directly to vertex input instead of passing them through a uniform. This avoids making too many uniform calls or exceeding the limit on the number of uniform variables.

layout(location = 5) in mat4 aModelMatrix;

The instancing method greatly reduces the number of drawcalls performed by my geometry pass, thus speeding up its execution time.

Frustum Culling.

To determine whether an object is visible or not, I use a naive implementation of frustum culling. Frustum culling is a method that determines whether an object is in the camera’s field of view (the camera’s frustum). If an object doesn’t appear on camera, we don’t need to draw it. To find out if a mesh is in my camera’s field of view, I need to calculate the volume of the frustum, create a bounding volume around each mesh and see if it’s inside the frustum.

I’ve pre-calculated bounding sphere volumes for each of my meshes using this algorithm:

void Mesh::GenerateBoundingSphere() {
    glm::vec3 min_aabb = glm::vec3(std::numeric_limits<float>::max());
    glm::vec3 max_aabb = glm::vec3(std::numeric_limits<float>::min());
  
    for (const auto& vertex : vertices_) {
      min_aabb.x = std::min(min_aabb.x, vertex.position.x);
      min_aabb.y = std::min(min_aabb.y, vertex.position.y);
      min_aabb.z = std::min(min_aabb.z, vertex.position.z);
  
      max_aabb.x = std::max(max_aabb.x, vertex.position.x);
      max_aabb.y = std::max(max_aabb.y, vertex.position.y);
      max_aabb.z = std::max(max_aabb.z, vertex.position.z);
    }
  
    glm::vec3 center = 0.5f * (min_aabb + max_aabb);
    float radius = glm::length(max_aabb - min_aabb) * 0.5f;
  
    bounding_volume_ = BoundingSphere(center, radius);
}

Then I calculate the frustum of my camera with plane objects like so:

// Half vertical side.
const float far_half_v_side = far_ * std::tan(glm::radians(fov_ * 0.5f));
// Half horizontal side.
const float far_half_h_side = far_half_v_side * aspect_ratio;

const glm::vec3 front_mul_far = far_ * front_;

Frustum frustum;

// Near and Far plane.
frustum.near_face = Plane(position_ + near_ * front_, front_);
frustum.far_face = Plane(position_ + front_mul_far, -front_);

// Right and Left plane.
frustum.left_face = Plane(
    position_, glm::cross(front_mul_far - right_ * far_half_h_side, up_));
frustum.right_face = Plane(
    position_, glm::cross(up_, front_mul_far + right_ * far_half_h_side));

// Top and Bottom plane.
frustum.bottom_face = Plane(
    position_, glm::cross(right_, front_mul_far - up_ * far_half_v_side));

frustum.top_face = Plane(
    position_, glm::cross(front_mul_far + up_ * far_half_v_side, right_));

Finally with this math trick I can determine if a bounding sphere volume of a mesh is inside the frustum:

float Plane::CalculatePointDistanceToPlane(const glm::vec3& point) const {
    return glm::dot(normal_, point) - distance_;
}
  
// Call this function for each of the 6 frustum's planes.
bool BoundingSphere::IsOnOrForwardPlane(const Plane& plane) const {
    const auto distance = plane.CalculatePointDistanceToPlane(center_);
    return distance > -(radius_);
}

This method allows me to draw only the objects visible on the screen in my G-Buffer. This considerably reduces the number of drawing calls and the execution time of my geometric pass.

SSAO Pass

SSAO stands for Screen Space Ambient Occlusion. It’s a technique used to enhance the realism of 3D scenes by simulating the subtle shadows that occur in creases, corners, and tight spaces due to ambient lighting. I’m not going to go into the technical details of this method, as that would take too long to explain, but rather the general idea and the result.

As mentioned above, the algorithm needs the view-space positions and normals of each pixel in the scene. This information is stored in the first two textures of the G-Buffer. The algorithm will simulates ambient occlusion by analyzing the depth and normal information of neighboring pixels on the screen. It calculates how likely it is for each pixel to be occluded by nearby geometry, based on how close together the surfaces are. It darkens the pixels where occlusion occurs, creating a more realistic shading effect that makes the scene look more natural and detailed.

To have a better result, the method use a kernel sample table containing sample points representing directions from the current pixel to surrounding areas. By taking multiple samples around each pixel, SSAO can better estimate the occlusion contribution from nearby geometry. The size and distribution of these samples affect the quality and accuracy of the SSAO effect.

The algorithm also take into account a 4x4 array of random rotation vectors oriented around the tangent-space surface normal called a noise texture to reduce the number of samples necessary to get good results.

Noise Texture

The result of the SSAO is stored in the red channel of a framebuffer’s texture and looks like that:

SSAO Map

To soften shadows and avoid noisy results, a blurring algorithm is then applied to the ssao texture.

Blurred SSAO Map

Shadow Mapping Pass

Shadow mapping is a technique for determining whether or not an object is in shadow from the point of view of light. To do this, the scene is rendered from the light’s point of view in a depth map and everything we see from the light’s perspective is lit and everything we can’t see must be in shadow.

This pass doesn’t do the light calculations, it just encompasses the pipelines and drawcalls creating the shadow maps of the lights in my scene, which are a directional light and a point light. The different shadow maps will then be given to the PBR pipeline which applies the light in the scene, but we will see that later.

Also note that as I write this blog post, my entire scene is static, which is why I create the shadow maps only once at the start of my program. There is no point in redrawing the scene if it is the same every frame.

Directional Light Shadow Map

To create the shadow map from the perspective of the directional light a light-space matrix is ​​necessary. This matrix is created using an orthographic projection matrix and a view matrix using different data such as the position and direction of the light. An orthographic projection matrix is perfect for simulating parallel rays of light. That’s what you want when you’re creating directional light.

glm::mat4 light_projection = glm::ortho(-width, width, -height, height, near_plane, far_plane);
glm::mat4 light_view = glm::lookAt(light_pos_, light_pos_ + light_dir_, glm::vec3(0.0, 1.0, 0.0));
light_space_matrix_ = light_projection * light_view;

Also note that to avoid the Peter Panning problem, the front faces of the meshes are culled.
The result of the directional light shadow map looks like this:

Directional Light Shadow Map

Point Light Shadow Cubemap

To create the shadow map of a point light, there is more work required. Indeed this time the light does not have only one direction. It is therefore necessary to render the scene from all surrounding directions of a point light. A basic approach to obtain this result is to use a cubemap, because a cubemap can store full environment data with only six faces, it is possible to render the entire scene to each of the faces of a cubemap and sample these as the point light’s surrounding depth values

As before, a light-space matrix is ​​required but this time a perspective projection matrix is ​​used. In addition, you must create 6 light-space matrices for the 6 faces of the shadow cubemap.

for (int i = 0; i < 6; i++) {
    light_view = glm::lookAt(point_light.position,
                             point_light.position + light_dirs[i], light_ups[i]);

    light_projection = glm::perspective(glm::radians(90.f), shadow_map_aspect,
                                        kLightNearPlane, kLightFarPlane);

    point_light_space_matrix_ = light_projection * light_view;
}

As before the front faces are culled to avoid Peter Panning and there is the result of the shadow cubemap:

X+	X-	Y+
Y-	Z+	Z-

The depth maps are upside down because of the way OpenGL cube maps work. They assume that the origin of the images is at the top left. This is why things are reversed in the Y direction.

PBR Pass

This is when things get really serious. This pass is the one that applies all the light calculations with the shadows. All the data created and stored in the past will be used at this point. The light caclulation technique used in my scene is PBR (Physically Based Rendering), specifically the approach that has been explored by Disney and Epic Games. I’m not going to go into the mathematical and technical details, as I’m absolutely not the person best qualified to do so, and it would take far too much time. But I will try to explain the basic principles.

The PBR approach aims to mimic light in a physically plausible way by following three conditions:

1. Be based on the microfacet surface model.
2. Be energy conserving.
3. Use a physically based BRDF (Bidirectional Reflective Distribution Function).

PBR also uses two fundamental material properties to simulate how objects react to light in a physically based way:

• The roughness of the object.
• The metalness of the object.

The roughness of an object will determine the alignment of the surface microfacets, which are tiny little perfectly reflective mirrors, more or less dispersing incoming light rays. The more the microfacets are aligned to the vector sitting halfway between the light and view vector, the sharper and stronger the specular reflection.

The metalness of an object will help to describe the material’s basic reflectivity index.

The bidirectional reflection distribution function is an approximation of the contribution of light rays to the final reflected light based on the material’s physical properties (roughness and metalness).

With all these data and concepts, we can, using complex mathematics that I’ll hide for the purposes of this post, calculate the reflected sum of the irradiance of each light on each fragment seen from the camera view vector.

This is obviously an extremely simplified summary describing the main principles of PBR, so I’ll leave you to find out for yourself if you want to know the details. Here’s learnopengl’s article on the subject: https://learnopengl.com/PBR/Theory

Lights and Shadows

To perform light calculations, you need to know the position of each fragment, the normal and the texture of the PBR material. All these data have been stored in the G-Buffer, but in view-space, so we’ll need to read and convert them using the inverse of the view matrix. This is also when you need to read the SSAO values to add ambient occlusion and the various shadow maps to apply shadows.

So this is the most important inputs needed for light calculation in the PBR fragment shader:

// G-buffer values.
uniform sampler2D gViewPositionMetallic;
uniform sampler2D gViewNormalRoughness;
uniform sampler2D gAlbedoAmbientOcclusion;
uniform sampler2D gEmissive;

uniform sampler2D ssao;

uniform sampler2D shadowMap; // directional light shadows.
uniform samplerCube shadowCubeMap; // point light shadows.

uniform mat4 inverseViewMatrix;

Data is read and converted as follows:

vec3  albedo    = texture(gAlbedoAmbientOcclusion, texCoords).rgb; // loaded in SRGB
float metallic  = texture(gViewPositionMetallic, texCoords).a;
float roughness = texture(gViewNormalRoughness, texCoords).a;
float ao        = texture(gAlbedoAmbientOcclusion, texCoords).a;
float ssao = texture(ssao, texCoords).r;

float combined_ao = ssao * ao;

vec3 fragViewPos = texture(gViewPositionMetallic, texCoords).rgb;
vec4 fragWorldPos = inverseViewMatrix * vec4(fragViewPos, 1.0);

vec3 viewNormal = texture(gViewNormalRoughness, texCoords).rgb;
vec3 worldNormal = mat3(inverseViewMatrix) * viewNormal;

vec3 worldViewDir = normalize(viewPos - vec3(fragWorldPos));
vec3 reflection = reflect(-worldViewDir, worldNormal);

Then the mathematics of the PBR method are applied to calculate the color of each fragment based on the lights in the scene. The mathematical equation used to simulate the visuals of light is the Cook-Torrance Reflectance Equation. What it does is it sums up the reflected irradiance of the light on a fragment. My goal is not to explain this equation in detail but rather to explain the purpose behind it to understand how light is calculated in my scene.

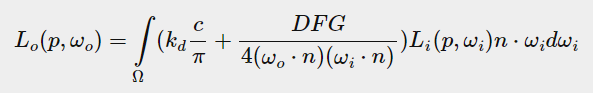
Cook-Torrance Reflectance Equation (this way we know what it looks like).

Finally, shadows are calculated by comparing the depth values of the various shadow maps with those of the fragments, and doing a little mathematics. The resulting shadow value lies between 0 and 1, and is used to define the percentage by which a fragment is in shadow, in order to reduce the intensity of light it receives. The final light calculation looks like this in pseudo-code:

// Irradiance -> amount of radiant energy (light in this context) incident on the fragment.
vec3 Lo = vec3(0.0);

float directional_light_shadow = CalculateDirectionalLightShadow();
Lo += (1.0 - directional_light_shadow) * CalculateDirectionalLightRadiance();

float point_light_shadow = CalculatePointLightShadow();
Lo += (1.0 - point_light_shadow) * CalculatePointLightRadiance();

Here’s the result after calculating the directional light:
(Note that my implementation of emissive material is extremly basic and naive. I simply force the emissive color to be displayed over the other colors after light calculation. Basically, I treat emissive textures as a material that emits light of its own accord. It is virtually unaffected by surrounding lights.)

Directional Light

And here’s the result after calculating the point light:

Point Light

For the moment, everything looks rather dark because the textures are load in SRGB space to avoid problems with the monitor output, a gamma correction will be applied to pixel color and the shadows and colors of the scene will be much more visible, but I’ll talk about this later in the HDR pass.

IBL

We’re not done with light calculations yet. For the moment, objects react to light based on their material properties. However, these lights are direct analytical lights, but in real life, objects are also illuminated by the ambient light of the environment. To simulate the environment ambient lighting, a technique known as IBL (Image Based Lighting) is used. This method is accomplished by manipulating a cubemap environment map (taken from the real world or generated from a 3D scene) such that we can directly use it in our lighting equations, treating each cubemap texel as a light emitter.

The type of image file used to create the cube map is is the “.hdr”. This format allows us to specify color values outside the 0.0 to 1.0 range of the monitor, to give lights their correct color intensities. However, this type of image is a large rectangle called an equirectangle.

Equirectangular Map

(As before, the images I will show are a bit dark because of the fact that they are loaded in SRGB space so their color are not the correct one for now.)

So the first step is to convert this equirectangular map to a cubemap with an algorithm performed on a fragment shader:

X+	X-	Y+
Y-	Z+	Z-

Now we need to approximate the value of the integral of the reflectance equation for an arbitrary number of sample directions (because we cannot calculate the value for all directions of light because they are infinite). But to make the work easier, we can split the intergal in two, with one part for the diffuse term and the other for the specular term like so:

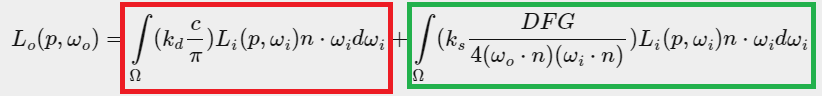
Cook-Torrance Reflectance Equation split in two part:
In red: the diffuse term part
In green: the specular term part

Here too the goal is not to understand the math behind this equation but rather the principle of separating it into two distinct parts to focus on each in due time.

Now we can calculate the result for all sampled directions specificly for the diffuse term of the equation. These results are pre-calculated and stored at the start of the program in a cubemap called the irradiance map. This allows us to directly find the value of the desired integral in the cubemap for our light calculations. This cubemap represents somewhat the average color of the ambient lighting of the environment. Here is how the irradiance map looks like:

X+	X-	Y+
Y-	Z+	Z-

The next step is to calculate the specular term of the equation. To do this, the work is separated into two parts.

The first part will create a cubemap called the pre-filtered environment map. This map is similar to the irradiance map but this one takes roughness of the material into account. For increasing roughness levels, the environment map is convoluted with more scattered sample vectors, creating blurrier reflections. For each roughness level, a mipmap level of the cubemap is created, in the case of my scene there is five mipmap levels. Which means that each level of mipmap is more and more blurry and pixelated.

Here is the first mipmap level of my pre-filtered environment map:

X+	X-	Y+
Y-	Z+	Z-

The second part of the specular term calculates the BRDF part of the equation. The objective is to pre-calculate the BRDF values ​​for a good number of roughness values. Epic Games stores the pre-computed BRDF’s response to each normal and light direction combination on varying roughness values ​in a 2D lookup texture (LUT) known as the BRDF integration map.

BRDF Lookup texture

The red channel represents the x-axis and is treated as as the BRDF’s input which is the angle between view direction and normal.
The green channel represents the y-axis and is treated as the input roughness value.

Now we can finally calculate the ambient lighting based on the environment by sending all these textures to the PBR fragment shader and read their data to obtain the inputs for the light calculation. The final output looks like this:

The scene using IBL

We can clearly see the impact of the IBL method on the golden spheres as they reflect the environment due to their metallic proprety.

Front Shading Pass

This pass is much simpler to understand than the previous one, fortunately. Quite simply, this pass draws the objects that are not impacted by the light calculations, so these objects have not been drawn in the G-Buffer. In my scene, there’s the point light itself and the sky box. The aim of this render pass is to draw these objects in the scene without overwriting the objects already drawn.

This is why we have to copy the depth content of the G-Buffer before drawing any new object:

g_buffer_.BindRead();
hdr_fbo_.BindDraw();
glBlitFramebuffer(0, 0, screen_size.x, screen_size.y, 0, 0, screen_size.x,
                  screen_size.y, GL_DEPTH_BUFFER_BIT, GL_NEAREST);

You can see that the data are not copied on the backbuffer but on a frame buffer which I’ve called “hdr_fbo” that stands for High Dynamic Range Framebuffer. This is because all pixel are in a non-linear space so their color aren’t the correct one for now. The goal is to store all the scene in this hdr_fbo and then correct all the pixels at once at the last render pass that we will see later.

So now the point light is drawn on the scene:

Scene Map with Point Light

Then it is time to draw the skybox but there is a little trick. In fact, drawing the skybox last is a good optimization, because with the depth values of objects already present in the scene, the early depth test can discard fragments saving us valuable bandwidth. However, for this to work, it is necessary that the Z value of each pixel be equal to 1.0, for the depth test to fail wherever there’s a different object in front of it. It is also necessary to modify the depth function by setting it to “GL_LEQUAL” instead of the traditional “GL_LESS”.

// w instead of z to always have a z value of 1.
gl_Position = clipPos.xyww;

Now the skybox can be rendered in a proper way:

Scene Map with Skybox

Now we are done with rendering the scene. The last steps are just post-processing.

Bloom Pass

One of the most famous post-processing effect is certainly the bloom. In my scene I implemented a physically based bloom effect thanks to this article https://learnopengl.com/Guest-Articles/2022/Phys.-Based-Bloom from “Alexander Christensen”

Bloom gives all brightly lit regions of a scene a glow-like effect. It aims to simulate the behavior of the human eye or a camera lens when it encounters bright light sources. It means that we need a way to exctract the brightest pixels of the scene to apply post-processing bloom effect on them.

And this is where I admit not having said everything in the last two render passes. Indeed during the PBR and Front Shading pass, each pixel was drawn in the famous “hdr_fbo” presented earlier. This frame buffer contains two color attachments. The first is a texture which contains all the pixels of the scene while the second contains only the bright pixels of the scene (those whose value exceeds 1.0).

It was done by a simple color check like so:

// check whether result is higher than some threshold, if so, output as bloom threshold color
float brightness = dot(color, vec3(0.2126, 0.7152, 0.0722));

if(brightness > 1.0)
    brightColor = vec4(color, 1.0);
else
    brightColor = vec4(0.0, 0.0, 0.0, 1.0);

fragColor = vec4(color, 1.0);

First color attachment of the HDR FBO containing the pixels of the scene

Second color attachment of the HDR FBO containing the bright pixels of the scene

I didn’t say it earlier because I didn’t want to give too much information at once.

The way bloom is applied in the article from “Alexander Christensen” is by applying a down-sampling algorithm which runs a shader which downsamples (downscales) the HDR buffer containing per-pixel color. This shader is run a fixed number of times to continually produce a smaller image, each time with half resolution in both X and Y axes.

Down Mip 1: 640x360

Down Mip 3: 160x90

Down Mip 5: 40x22

Then it runs a small 3x3 filter kernel on each downsampled image, and progressively blur and upsample them until we reach the first image.

Up Mip 2: 160x90

Up Mip 4: 640x360 (final bloom image)

That’s all for creating the bloom texture. All that remains is to send it to the last render pass which will be responsible for mixing this texture with the texture of the scene.

HDR Pass

Finally here is the famous HDR render pass that I have been talking about for a while now. HDR stands for High Dynamic Range which is a value range beyond the traditional range of monitors going from 0.0 to 1.0. This makes it possible to represent very intense lights exceeding the value of 1.0 and allows more precise and consistent light calculations. However, we must not forget that the monitors are in Low Dynamic Range. It is therefore necessary to convert the values ​​into LDR with a tone mapping algorithm before the final render.

An other calcul is applied to pixels before the last render. This calcul is the “gamma correction” that I already mentionned a bit. Gamma correction compensates the non-linear relationship between pixel intensity values and perceived brightness on monitors. So as I already said, all the textures of my scene were loaded in SRGB space, which is a non-linear space, to perform better light calculations and to manage gamma correction myself in due time.

This render pass is therefore responsible for mixing the scene texture with the bloom texture, applying a gamma correction to the pixels and converting the pixel values ​​from HDR to LDR. This is the final process of my scene.

Here is the two textures which will be mixed together:

First color attachment of the HDR FBO containing the pixels of the scene

Bloom texture

So here’s the latest post-process applied to the rendering of my scene. First, the texture of the bloom is mixed with that of the scene. Then a tone mapping algorithm is applied to the fragments to convert them from HDR to LDR. Personnaly I use the “Narkowicz ACES” tone mapping algorithm. Finally, gamma correction is applied to the fragments to bring them back into linear space.

const float gamma = 2.2;
vec3 hdrColor = texture(hdrBuffer, texCoords).rgb;
vec3 bloomColor = texture(bloomBlur, texCoords).rgb;
vec3 mixed_color = mix(hdrColor, bloomColor, bloomStrength); // linear interpolation;

// Narkowicz ACES tone mapping
mixed_color *= 0.6;
vec3 mapped = (mixed_color * (2.51f * mixed_color + 0.03f)) /
              (mixed_color * (2.43f * mixed_color + 0.59f) + 0.14f);
mapped = clamp(mapped, vec3(0.0), vec3(1.0));

// gamma correction
mapped = pow(mapped, vec3(1.0 / gamma));
fragColor = vec4(mapped, 1.0);

Now the rendering process is finally complete. Here is the final result of the scene:

Final Result mixing the scene map and the bloom map with tone mapping and gamma correction.

Conclusion

What a lot of work to create a 3D scene, right ? Certain steps could have been carried out in a more modern and optimal way, notably by using compute shaders. However I wanted to stay in the version 300 es of OpenGL to have the opportunity to port my scene to the web with emscripten. There are also other additions that I would like implemented in my scene such as a TAA (Temporal Anti-Aliasing) algorithm because when the camera is moved, you can see a lot of small pixel glitches.

I would also like to be able to load models in FBX format because the OBJs have had their day.

Also my program takes way too long to load textures and models at first. I would have to optimize that with multi-threading for example.

But despite that, I’m very pleased with the final result and I hope that my explanations were clear enough and pleasant enough to read.

If you are interested in the code of my scene or want to see it, here is my github: https://github.com/Chocolive24/3D_OpenGL_Scene

If you want to see in more detail how certain concepts work more precisely I refer you to the incredible learnopengl site which helped me enormously during my learning journey: https://learnopengl.com/

Thank you for taking the time to read.