
The optimizations I made to my 2D C++ physics engine
Physics Optimization C++ Engine 2D SAE
Hello, welcome to this blog dedicated to optimization. I’m a Swiss student at the Sae Institute in Geneva and as part of a graded assignment, we’ve been asked to program a 2D physics engine and optimize a part of it. This specific part is the detection of intersections between colliders in trigger state. We have a scene containing physical bodies to which colliders are attached in trigger mode. The aim is to make this scene with a thousand circles run as smoothly as possible.
In this blog, I’m going to do some research to optimize my engine, show and explain them, and then do some statistical tests to prove that the changes I’ve made do indeed make the program faster.
The software I will use to profile my engine is “Tracy”: https://github.com/wolfpld/tracy
I already implemented some ZoneScoped in my code to be able to see the hot path of my program in tracy. I will not teach you how tracy works so I let you check the documentation of Tracy if your interested by this software.
If you are interested in my project, here is the link to the github repository: https://github.com/Chocolive24/PhysicsEngine
Actual state of the engine.
To handles bodies and colliders in my engine I have these data structures in my World class:
// Custom allocator that traces the allocations and deallocations.
HeapAllocator _heapAllocator;
// The "AllocVector" type that is used in every of my data structures is an std::vector using my own custom standard allocator
// that calls the "_heapAllocator" in order to trace my allocations with tracy.
// Vector which stores all bodies.
AllocVector<Body> _bodies{ StandardAllocator< Body >{_heapAllocator} };
// Vector which stores the generation index of each body.
// This system of index keeps track of changes to bodies and prevents the use of outdated references.
AllocVector< std::size_t > _bodiesGenIndices{ StandardAllocator< std::size_t >{_heapAllocator} };
// Vector which stores all colliders.
AllocVector< Collider > _colliders{ StandardAllocator<Collider>{_heapAllocator} };
// Vector which stores the generation index of each collider.
// This is the same system as the one for the bodies.
AllocVector< std::size_t > _collidersGenIndices{ StandardAllocator< std::size_t >{_heapAllocator} };
// Unordered_set that stores all the pairs of overlapping colliders.
// I use an unordered_set because it can't contains the same pair two times.
// It enables me to insert and remove pairs easily.
std::unordered_set< ColliderPair,
ColliderHash,
std::equal_to< ColliderPair >,
StandardAllocator< ColliderPair > > _colliderPairs{ StandardAllocator< ColliderPair >{_heapAllocator} };If you are interested in how I implemented my custom allocators, here is the source code: https://github.com/Chocolive24/PhysicsEngine/blob/master/common/include/Allocator.h
When I’m outside the world class, I access my collider using a “ColliderRef” type that stores the index of a collider in the “_colliders” vector and the generation index of this collider. My “ColliderPair” class typically uses two “ColliderRef” to be able to tell which collider overlap which other collider:
/**
* @brief ColliderRef is a struct used to reference a specific collider.
* @brief Attributes :
* @brief Index : The index of the collider inside the world colliders vector.
* @brief GenerationIdx : The index inside the world colliders generation indices vector.
*/
struct ColliderRef
{
std::size_t Index;
std::size_t GenerationIdx;
constexpr ColliderRef& operator=(const ColliderRef& colRef) noexcept = default;
constexpr bool operator==(const ColliderRef& other) const noexcept
{
return Index == other.Index && GenerationIdx == other.GenerationIdx;
}
};
/**
* @brief ColliderPair is a class that represents a pair of colliders for collision detection.
*/
struct ColliderPair
{
ColliderRef ColliderA;
ColliderRef ColliderB;
bool operator==(const ColliderPair& other) const noexcept
{
return ColliderA == other.ColliderA && ColliderB == other.ColliderB ||
ColliderA == other.ColliderB && ColliderB == other.ColliderA;
}
};At the moment here is the function responsible for triggering events related to overlapping pairs, and for maintaining a set of active collider pairs.
void World::detectColliderPairs() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
for (std::size_t i = 0; i < _colliders.size(); i++)
{
auto& colliderA = _colliders[i];
for (std::size_t j = i + 1; j < _colliders.size(); j++)
{
auto& colliderB = _colliders[j];
// Create the pair that may overlap.
ColliderPair possiblePair{ ColliderRef{i, _collidersGenIndices[i]}, ColliderRef{j, _collidersGenIndices[j]} };
// Detect if they overlap or not.
// The function simply take the type of shape of the collider and do the calculs to see if there is a contact between
// those colliders. For circles the calcul is : c1 + c2 <= r1 + r2
const auto doCollidersIntersect = detectContact(colliderA, colliderB);
#ifdef TRACY_ENABLE
ZoneNamedN(FindPair, "Find pair", true);
#endif
// Try to find the pair inside the current world's pairs.
auto it = _colliderPairs.find(possiblePair);
#ifdef TRACY_ENABLE
ZoneNamedN(CheckIfItsANewPair, "Check if it's a new pair", true);
#endif
// If the pair is already stored in the world's current pairs.
if (it != _colliderPairs.end())
{
// If they don't intersect anymore -> activate TriggerExit event.
if (!doCollidersIntersect)
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerExit(possiblePair.ColliderA,
possiblePair.ColliderB);
}
#ifdef TRACY_ENABLE
ZoneNamedN(ErasePair, "Erase pair", true);
#endif
// Remove the pair of the current world's pairs.
_colliderPairs.erase(it);
}
// If they always intersect -> activate TriggerStay event.
else
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerStay(possiblePair.ColliderA,
possiblePair.ColliderB);
}
}
}
// If the pair is not stored in the world's current pair.
else
{
// If they intersect -> activate the TriggerEnter event.
if (doCollidersIntersect)
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerEnter(possiblePair.ColliderA,
possiblePair.ColliderB);
}
#ifdef TRACY_ENABLE
ZoneNamedN(InsertPair, "Insert pair", true);
#endif
// Add the new pair to the world's current pairs.
_colliderPairs.insert(possiblePair);
}
}
}
}
}To demonstrate that the collider trigger system works, I’ve made a sample that instantiates objects with random velocities and trigger colliders. The objects are initially red and turn green when they overlap another object.
Let’s take a look at how this sample runs with 3 different total numbers of colliders, once with 100 colliders, then 500 and finally with 1000 colliders. :
  
As you can see, the sample runs fine with 100 objects, is a bit slow with 500 objects and very slow with 1000 objects. From now and till the end of this blogpost I’ll use the sample with 1000 objects as a reference to compare the execution speed of my program after each optimization I make. My goal is to run my sample with 1000 objects or more.
Creation of a broad-phase.
When it comes to detecting contact or overlap between bodies in a physics engine, two distinct phases stand out.
The first one is the broad phase which is the first stage of collision detection and serves the purpose of quickly reducing the number of potential collision pairs to a manageable subset.
The second one is the narrow phase which is the second stage of collision detection and is responsible for determining the precise details of the collisions between pairs of objects identified in the broad phase.
By now I only have a sort of narrow phase that checks each collider with each other. The current complexity of my function is O(n^2). Let’s try to reduce this complexity by removing the pairs that for sure will never overlap.
Sub-dividing the world with a quad-tree.
For the moment, I’m comparing each collider with each other, even if they’re far apart. It means that if a collider is in the bottom-left-corner of the world space and another one is in the up-right-corner, my function would compare them. But it is cleary uneccassary to check this pair.

It would be nice if I compare only the colliders that are in a same zone of the world space. So I need to subdivide the world space to have less check to do.
One way to do it is to subdivide the current world space in 4 subspaces and then compare only colliders in their subspace with other colliders in that subspace.
 
Okay that’s cool, like that I avoid unessary checks. At least as long as there aren’t too many colliders in the same zone.

To be more efficient, I can subdivide the world recursively to have as few comparisons as possible. It will greatly reduces the number of potential collider pair to manage.
This method of space subdivision is called “quad-tree”. I can represent a quad-tree as a tree with a root node with 4 children nodes that have 4 children nodes too etc recursively:
 
Before implementing a quad-tree in my engine, there is a last thing to take in considereration. It is the case where two colliders are perfectly between several sub-spaces. If I add them in each of the subspaces they touch, I’ll check them several times in several subspaces. This would duplicate the pair in the different nodes and give us a bad result. That’s why, in this case, it’s better to add these colliders to the parent node.
 
Well, I don’t think I’ve forgotten anything. I’ll try to implement a quad-tree in my program.
Quad-tree implementation
In the rest of the blog post, you’ll often see types and functions from a namespace called “Math”. This namespace contains everything you need to calculate intersections of geometric shapes and other useful notions.
If you really don’t understand what certain types or functions do, I’ll let you have a look at the source code: https://github.com/Chocolive24/PhysicsEngine/tree/master/libs/math/include
So to implement a quad-tree I need 2 classes.
The first one is a QuadNode class (I did a struct because all elements need to be public) that will looks like that:
Note that the pointers I use to create child nodes are of type “UniquePtr”, which is my custom type that allows me to trace my allocations. You can replace them with “std::unique_ptr”. If you’re interested in how this class is implemented, here’s the source code: https://github.com/Chocolive24/PhysicsEngine/blob/master/common/include/UniquePtr.h
/**
* @brief QuadNode is a struct representing a node in a quad-tree data structure used for spatial
partitioning in a 2D space.
*/
struct QuadNode
{
/**
* @brief MaxColliderNbr is the maximum number of colliders that the node can stores before a subdivision
* of the world.
*/
static constexpr int MaxColliderNbr = 8;
/**
* @brief BoundaryDivisionCount is the number of space boundary subdivision for the node.
*/
static constexpr int BoundaryDivisionCount = 4;
Math::RectangleF Boundary{Math::Vec2F::Zero(), Math::Vec2F::Zero()};
// The UniquePtr type for the children node is my custom unique pointer implementation
// which uses my custom HeapAllocator to be able to trace allocations.
std::array<UniquePtr< QuadNode >, BoundaryDivisionCount > Children;
AllocVector< SimplifiedCollider > Colliders{};
//constexpr QuadNode() noexcept = default;
explicit QuadNode(Allocator& allocator) noexcept :
Colliders{ StandardAllocator< SimplifiedCollider > {allocator} } {}
};The second one is the quad-tree class:
/**
* @brief QuadTree is a class that represents a quad-tree used for spatial partitioning of the world space.
*/
class QuadTree
{
private:
HeapAllocator _heapAllocator;
UniquePtr< QuadNode > _rootNode;
// Vector that contains all possible pairs of collider in the tree.
AllocVector<ColliderPair> _possiblePairs{ StandardAllocator<ColliderPair> {_heapAllocator} };
/**
* @brief MaxDepth is the maximum depth of the quad-tree recursive space subdivision.
*/
static constexpr int _maxDepth = 5;
};Also I created an “Init” method to initialize the quad-tree and a “Clear” method that reset the quad-tree at the start of each frame:
void QuadTree::Init() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif // TRACY_ENABLE
_rootNode = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
}
void QuadTree::Clear() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif // TRACY_ENABLE
_rootNode = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
_possiblePairs.clear();
}Create the root node.
The first thing I need to create for the quad-tree is the root node.
The root node will encompass all the colliders in the world and serve as the basis for the sub-division. To find the size of the root node, I need to search for the body with the smallest X position and the body with the smallest Y position, then similarly we need to search for the body with the largest X position and the body with the largest Y position. I know from this search that there are no bodies outside the rectangle created by these 4 positions.
QuadTree.h
void SetRootNodeBoundary(const Math::RectangleF boundary) noexcept
{
_rootNode->Boundary = boundary;
};World.cpp
void World::resolveBroadPhase() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
#ifdef TRACY_ENABLE
ZoneNamedN(SetRoodNodeBoundary, "SetRootNodeBoundary", true);
ZoneValue(_colliders.size());
#endif
_quadTree.Clear();
// Sets the minimum and maximum collision zone limits of the world rectangle to floating maximum and
// lowest values.
Math::Vec2F worldMinBound(std::numeric_limits<float>::max(), std::numeric_limits<float>::max());
Math::Vec2F worldMaxBound(std::numeric_limits<float>::lowest(), std::numeric_limits<float>::lowest());
// Adjust the size of the collision zone in the world rectangle to the most distant bodies.
for (const auto& collider : _colliders)
{
if (!collider.Enabled()) continue;
const auto colCenter = GetBody(collider.GetBodyRef()).Position();
if (worldMinBound.X > colCenter.X)
{
worldMinBound.X = colCenter.X;
}
if (worldMaxBound.X < colCenter.X)
{
worldMaxBound.X = colCenter.X;
}
if (worldMinBound.Y > colCenter.Y)
{
worldMinBound.Y = colCenter.Y;
}
if (worldMaxBound.Y < colCenter.Y)
{
worldMaxBound.Y = colCenter.Y;
}
}
// Set the first rectangle of the quad-tree to calculated collision area rectangle.
_quadTree.SetRootNodeBoundary(Math::RectangleF(worldMinBound, worldMaxBound));
}Insert colliders in the quad-tree.
The next step is to insert the colliders into my quad-tree. Each collider will be inserted recursively from the root node. To find out in which node a collider should be placed, I store the colliders in rectangular form, then add them to the node they overlap. Obviously, if a collider overlaps several nodes, it remains in the parent node.
/**
* @brief SimplifiedCollider is a struct that stores the data of a collider in a simplified way (aka it stores
* its collider reference in the world and its shape in a rectangle form).
*/
struct SimplifiedCollider
{
ColliderRef ColRef;
Math::RectangleF Rectangle;
};
I use 2 methods to insert colliders. A public method that takes a simplified collider and inserts it into the root node. This ensures that I never insert a collider anywhere other than the first node.
The other method is private and will be called recursively to insert colliders in the correct subspaces if they have been created.
void QuadTree::Insert(Math::RectangleF simplifiedShape, ColliderRef colliderRef) noexcept
{
insertInNode(*_rootNode, simplifiedShape, colliderRef, 0);
}
void QuadTree::insertInNode(QuadNode& node,
Math::RectangleF simplifiedShape,
ColliderRef colliderRef,
int depth) noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
// If the node doesn't have any children.
if (node.Children[0].Get() == nullptr)
{
// Add the simplified collider to the node.
SimplifiedCollider simplifiedCollider = { colliderRef, simplifiedShape };
node.Colliders.push_back(simplifiedCollider);
// If the node has more colliders than the max number and the depth is not equal to the max depth.
if (node.Colliders.size() > QuadNode::MaxColliderNbr && depth != _maxDepth)
{
#ifdef TRACY_ENABLE
ZoneNamed(SubDivision, "Sub-division", true);
#endif
// Subdivide the node rectangle in 4 rectangle.
const auto center = node.Boundary.Center();
const auto halfSize = node.Boundary.HalfSize();
const auto topMiddle = Math::Vec2F(center.X, center.Y + halfSize.Y);
const auto topRightCorner = center + halfSize;
const auto rightMiddle = Math::Vec2F(center.X + halfSize.X, center.Y);
const auto bottomMiddle = Math::Vec2F(center.X, center.Y - halfSize.Y);
const auto bottomLeftCorner = center - halfSize;
const auto leftMiddle = Math::Vec2F(center.X - halfSize.X, center.Y);
// Create the four children nodes.
node.Children[0] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[1] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[2] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[3] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
// Create the boundary of each children.
node.Children[0]->Boundary = Math::RectangleF(leftMiddle, topMiddle);
node.Children[1]->Boundary = Math::RectangleF(center, topRightCorner);
node.Children[2]->Boundary = Math::RectangleF(bottomLeftCorner, center);
node.Children[3]->Boundary = Math::RectangleF(bottomMiddle, rightMiddle);
// Vector that will contains the collider that overlap several nodes.
AllocVector<SimplifiedCollider> remainingColliders{ {_heapAllocator} };
for (const auto& col : node.Colliders)
{
int boundInterestCount = 0;
QuadNode* intersectNode = nullptr;
for (const auto& child : node.Children)
{
if (Math::Intersect(child->Boundary, col.Rectangle))
{
boundInterestCount++;
intersectNode = child.Get();
}
}
if (boundInterestCount == 1)
{
insertInNode(*intersectNode, col.Rectangle, col.ColRef, depth + 1);
}
else
{
remainingColliders.push_back(col);
}
}
node.Colliders.clear();
for (const auto& col : remainingColliders)
{
node.Colliders.push_back(col);
}
}
}
// If the node has children.
else
{
int boundInterestCount = 0;
QuadNode* intersectNode = nullptr;
// Iterates throw each children to know in which node to put the collider.
for (const auto& child : node.Children)
{
if (Math::Intersect(child->Boundary, simplifiedShape))
{
boundInterestCount++;
intersectNode = child.Get();
}
}
if (boundInterestCount == 1)
{
depth++;
insertInNode(*intersectNode, simplifiedShape, colliderRef, depth);
}
else
{
SimplifiedCollider simplifiedCollider = { colliderRef, simplifiedShape };
node.Colliders.push_back(simplifiedCollider);
}
}
}Then in my resolveBroadPhase method I simply iterate over all the colliders in my world, create their collider in simplified form and call the public “Insert” method. At the very end of my broad phase, I ask my quad-tree to calculate the possible pairs, so I only have to ask to retrieve them in my narrow phase.
// Inside the "resolveBroadPhase" function. Below the "SetRootNodeBoundary" code.
#ifdef TRACY_ENABLE
ZoneNamedN(InsertCollidersInQuadTree, "InsertCollidersInQuadTree", true);
ZoneValue(_colliders.size());
#endif
for (std::size_t i = 0; i < _colliders.size(); i++)
{
ColliderRef colliderRef = {i, _collidersGenIndices[i]};
const auto& collider = GetCollider(colliderRef);
if (!collider.Enabled()) continue;
const auto colShape = collider.Shape();
switch (colShape.index())
{
case static_cast<int>(Math::ShapeType::Circle):
{
#ifdef TRACY_ENABLE
ZoneNamedN(InsertCircle, "InsertCircle", true);
#endif
const auto circle = std::get<Math::CircleF>(colShape);
const auto radius = circle.Radius();
const auto simplifiedCircle = Math::RectangleF::FromCenter(
GetBody(collider.GetBodyRef()).Position(),
Math::Vec2F(radius, radius));
_quadTree.Insert(simplifiedCircle, colliderRef);
break;
} // Case circle.
} // Switch collider shape index.
} // For int i < colliders.size().
_quadTree.CalculatePossiblePairs();
Calculate all possible pair of colliders.
The last step in my quad-tree is to extract all possible pairs of overlapping colliders. To do this, I need to go down the tree from the root node and compare each collider in the parent node with all its children, then do the same thing again, going down the tree recursively to pass through all the nodes. To do this I have 3 methods.
The first method is public and allows the world to call for the creation of possible pairs. This method will then call the second method, which is private and will be called recursively on each node. The last method is also private and allows you to descend recursively on each child of a parent node to compare each collider of the parent with those of the children.
void QuadTree::CalculatePossiblePairs() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
calculateNodePossiblePairs(*_rootNode);
}
void QuadTree::calculateNodePossiblePairs(const QuadNode& node) noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
for (std::size_t i = 0; i < node.Colliders.size(); i++)
{
auto& simplColA = node.Colliders[i];
for (std::size_t j = i + 1; j < node.Colliders.size(); j++)
{
auto& simplColB = node.Colliders[j];
_possiblePairs.push_back(ColliderPair{ simplColA.ColRef, simplColB.ColRef });
}
// If the node has children, we need to compare the simplified collider with the
// colliders in the children nodes.
if (node.Children[0].Get() != nullptr)
{
for (const auto& childNode : node.Children)
{
calculateChildrenNodePossiblePairs(*childNode, simplColA);
}
}
}
// If the node has children.
// Go down to each children and compare each collider in the node and its children nodes.
if (node.Children[0].Get() != nullptr)
{
for (const auto& child : node.Children)
{
calculateNodePossiblePairs(*child);
}
}
}
void QuadTree::calculateChildrenNodePossiblePairs(const QuadNode& node, SimplifiedCollider simplCol) noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
// For each colliders in the current node, compare it with the simplified collider from its parent node.
for (const auto& nodeSimplCol : node.Colliders)
{
//if (Math::Intersect(simplCol.Rectangle, nodeSimplCol.Rectangle))
//{
_possiblePairs.push_back(ColliderPair{ simplCol.ColRef, nodeSimplCol.ColRef });
//}
}
// If the current node has children, we need to compare the simplified collider from its parent node with its children.
if (node.Children[0].Get() != nullptr)
{
for (const auto& child : node.Children)
{
calculateChildrenNodePossiblePairs(*child, simplCol);
}
}
}Now I simply need to replace my for loops in my “detectColliderPairs” method (which I call resolveNarrowPhase now) by a range loop threw the vector of possible pairs of the quad-tree. The rest of the code is the same, I try to find each possible pair in my unordered_set and activate the correct trigger events.
void World::resolveNarrowPhase() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif
const auto& possiblePairs = _quadTree.PossiblePairs();
#ifdef TRACY_ENABLE
ZoneValue(possiblePairs.size());
#endif
for (auto& possiblePair : possiblePairs)
{
// The same code as before
}
}Statistics after broad phase implementation
So let’s compare the old sample without the quad-tree and the new one with the quad-tree.
I created a function that draws the quad-tree by going down in each node recursively and that draws its boundary. You can check the sample’s source code to see how I did if you want to do it too: https://github.com/Chocolive24/PhysicsEngine/blob/master/samples/src/TriggerColliderSample.cpp
 
Visually, there’s a huge difference since the implementation of the quad-tree. Let’s compare the values of these two samples with tracy and calculate how much faster the second version is.
| Sample | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| without broad phase | 748.86 | 758.77 | 132.85 | 14 |
| with broad phase | 27.57 | 27.25 | 3.41 | 203 |
| [Table: Comparisons of narrow-phase statistics between the non-quad-tree and quad-tree versions.] |
The above values can be obtained directly using Tracy. However, we can’t say with these values if there is a significant difference between the means of two groups, although here the result seems fairly obvious given the huge difference between the statistics. Normally, to prove that there is a significant difference, we need to use the student t-test. This test compares two groups and assesses whether the observed differences between them are likely due to random chance or if they are statistically significant. The t-test defines a P value, usually at 5%, which is the probability that the null hypothesis is correct. If the test result is smaller than P (5%), this means that the null hypothesis has almost no chance of being correct. So let’s do a t-test on our values to find out the probability that the version of my engine without broad phase is better than the one with.
| P(T<=t) two-tail |
|---|
| 2.33e-17 |
| [Table: Student T-Test Values using P = 5%.] |
The “P” result of the T-Test proves that the probability that the version without broad phase is better is extremely close to 0. This tells us that there is indeed a significant time difference between the two versions, but it doesn’t tell us by how much.
To know the magnitude of this difference, we need to calculate the confidence interval. This is a range of values within which we are reasonably sure the true population parameter lies. This will show us how much time we save by making our broad phase between the worst and best cases.
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 753.6127898 | 12.37144189 | 26.72687524 | 726.8859145 | 780.339665 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
The confidence interval therefore lies between 726 ms and 780 ms. This means that in the worst case, we gain 726 ms with the broad phase, and in the best case, 780 ms. We’ve proved that this addition statistically improves the program.
Optimization of the quad-tree.
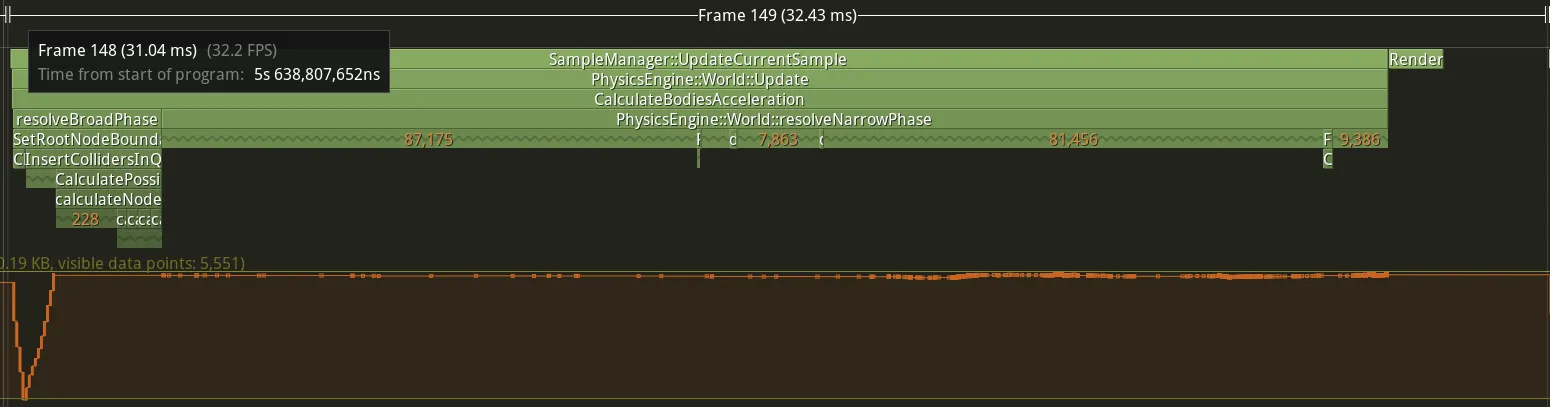
I have greatly reduced the execution time for collider pair detection. However, the time it takes to my engine to update is still over 16ms, which I don’t like. What can I improve in the code ? First, let’s look at the execution times of the different broad phase parts:
The three main part in the broad phase are:
- Clear to quad-tree
- Insert colliders in the quad-tree.
- Calculate all possible pairs of colliders.

Here is the different execution time of each part of the broad phase:
| Function name | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| Clear | 0.123 | 0.102 | 0.063 | 203 |
| Insert colliders | 3.23 | 3.17 | 0.494 | 203 |
| Calculate pairs | 2.59 | 2.53 | 0.477 | 203 |
| [Table: Statistics of each part of the broad phase] |
The longest part is the “Insert” one. So let’s analyse and investigate it. Perhaps there is something to do with the allocations of that part of the quad-tree.
Memory usage optimization
If we take a closer look at the “Insert” section, which is the longest, we see that there is a lot of allocations. There is a high number of deallocation in the clear part and a lot of allocation in the insert part. It because we are deleting and recreating unique pointers each time. This as a cost:
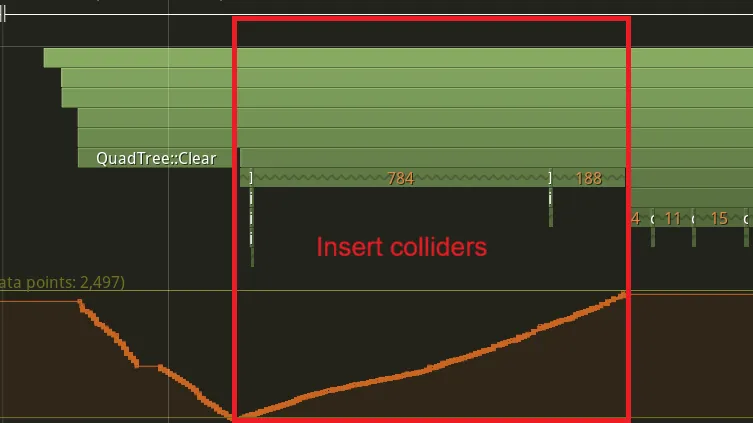
This allocations are made at each frame when we create the children nodes:
QuadTree.cpp -> insertInNode()
// begin of "insertInNode" function
node.Children[0] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[1] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[2] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
node.Children[3] = MakeUnique<QuadNode>(_heapAllocator, _heapAllocator);
// rest of "insertInNode" functionMaking memory allocations for each frame is definitely not the best idea. Whenever it’s possible to allocate memory at the beginning of the program and reuse the same memory block until the end, it’s crucial to do so. How can I allocate all the memory required for the children nodes at quad-tree initialization?
Pre-allocate all children nodes.
So I need to know how many nodes I need in the program. The number of nodes can vary, but I can know the maximum number of nodes. In fact, the quad-tree has a max depth that stops recursion. Using this max depth, I can know the maximum number of nodes and pre-allocate an equivalent amount at the start of the program.
The calcul is : 4^0 + 4^1 + 4^2 … + (4^{maxDepth}).
This gives the sum of each maximum node number on each level of the quad-tree, which is the maxmium of node possible. To store the memory of all these nodes, I’ll use a vector to call the resize function to directly create empty nodes and then perform push_back() easily. I also need a node index to find out where to place the chidlren nodes in memory.
QuadTree.h -> QuadTree class
class QuadTree
{
private:
AllocVector< QuadNode > _nodes{ StandardAllocator< QuadNode > {_heapAllocator} };
// Note that "_rootNode" becomes "_nodes[0]".
// The first child node has index 1 because the very first node is the root node which has index 0.
int _nodeIndex = 1;
// other attributes.
}So now the “Init” method will resize my vector with the maximum amount of node memory using a method that calculates this amount. In addition, the “Init” method reserves the maximum number of colliders (+ 1 to allow detection that I need to divide the node space) in each child’s vector of colliders. Finally, it also reserves an amount of memory in the vector of possible pairs. For the time being, there’s no mathematical way of knowing in advance the maximum amount of pairs possible. That’s why this value is totally arbitrary and I estimate it at three times the total number of nodes in the quad-tree.
template< typename T >
constexpr T QuadCount(T depth)
{
T result = 0;
for (T i = 0; i <= depth; i++)
{
result += Math::Pow(QuadNode::BoundaryDivisionCount, i);
}
return result;
}
void QuadTree::Init() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif // TRACY_ENABLE
const auto quadCount = QuadCount(_maxDepth);
_nodes.resize(quadCount, QuadNode({ _heapAllocator }));
_possiblePairs.reserve(quadCount * _possiblePairReserveFactor);
for (auto& node : _nodes)
{
node.Colliders.reserve(QuadNode::MaxColliderNbr + 1);
}
}Now that I have reserved the necessary memory for my quad-tree, I need to assign the children to these memory locations in the vector. The child nodes that were previously “UniquePtr” will now become simple raw pointers to locations in the node vector.
QuadTree.h -> QuadNode struct
struct QuadNode
{
// other attributes.
std::array< QuadNode*, BoundaryDivisionCount > Children{ nullptr, nullptr, nullptr, nullptr };
// other attributes.
}QuadTree.cpp -> insertInNode()
// Replace the MakeUnique() calls with this.
node.Children[0] = &_nodes[_nodeIndex];
node.Children[1] = &_nodes[_nodeIndex + 1];
node.Children[2] = &_nodes[_nodeIndex + 2];
node.Children[3] = &_nodes[_nodeIndex + 3];
_nodeIndex += 4;
node.Children[0]->Boundary = Math::RectangleF(leftMiddle, topMiddle);
node.Children[1]->Boundary = Math::RectangleF(center, topRightCorner);
node.Children[2]->Boundary = Math::RectangleF(bottomLeftCorner, center);
node.Children[3]->Boundary = Math::RectangleF(bottomMiddle, rightMiddle);Finally we need to change the “Clear” method. In addition to clearing the _possiblePairs vector and the colliders vector of each node, this methods need to reset the _nodeIndex to 1 and to fill all Children with null pointers:
QuadTree.cpp -> Clear()
void QuadTree::Clear() noexcept
{
#ifdef TRACY_ENABLE
ZoneScoped;
#endif // TRACY_ENABLE
for (auto& node : _nodes)
{
node.Colliders.clear();
std::fill(node.Children.begin(), node.Children.end(), nullptr);
}
_nodeIndex = 1;
_possiblePairs.clear();
}Let’s see if I have shortened the execution time of these various functions:
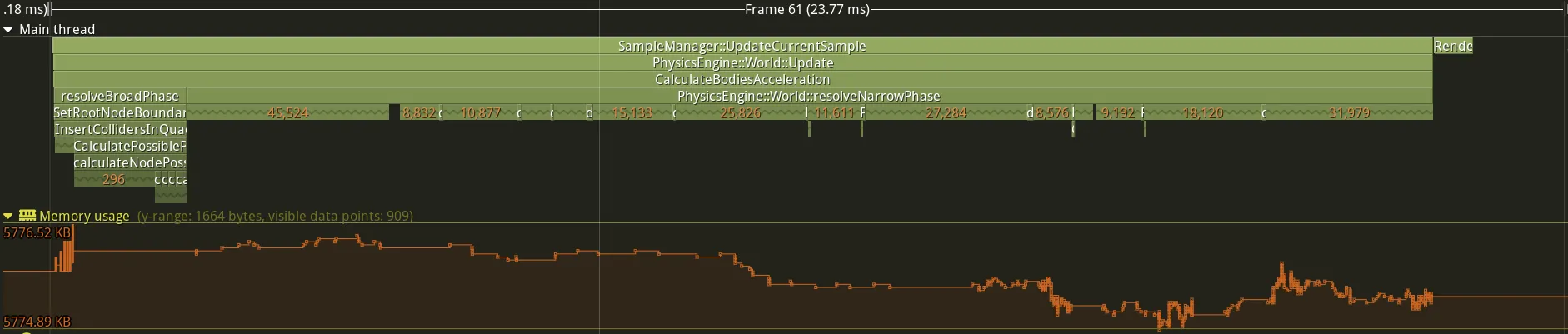
There is cleary less allocations as you can see on the image. I removed the large portion of allocations that formed a “V” at the beginning of the frame. Let’s analyse the statistics of the version 1 of the sample (without pre-allocation) and the version 2 (with pre-allocation):
| Sample version | Function name | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|---|
| Version 1 | Clear | 0.123 | 0.102 | 0.063 | 203 |
| Version 2 | Clear | 0.011 | 0.009 | 0.008 | 178 |
| Version 1 | Insert colliders | 3.23 | 3.17 | 0.494 | 203 |
| Version 2 | Insert colliders | 1.84 | 1.73 | 0.488 | 178 |
| Version 1 | Calculate pairs | 2.59 | 2.53 | 0.477 | 203 |
| Version 2 | Calculate pairs | 1.58 | 1.49 | 0.466 | 178 |
| [Table: Statistics of each part of the broad phase before and after the pre-allocation changes.] |
| Function name | P(T<=t) two-tail |
|---|---|
| Clear | 1.42e-64 |
| Insert colliders | 1.99e-129 |
| Calculate pairs | 8.49E-100 |
| [Table: Student T-Test Values using P = 5%.] |
The t-test tells us that each of the part of the broad phase has a significant difference as each value tends towards 0. So let’s see what that difference is:
| Function name | Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|---|
| Clear | 0.111309962 | 0.004471630267 | 0.008815035396 | 0.1024949266 | 0.1201249974 |
| Insert colliders | 1.395021166 | 0.03710855138 | 0.0729662906 | 1.322054876 | 1.467987457 |
| Calculate pairs | 1.009585563 | 0.03418671197 | 0.06722225855 | 0.9423633045 | 1.076807822 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
Note that the “Insert colliders” and “Calculate pairs” sections are about 1ms faster, which isn’t too bad. The “Clear” function, on the other hand, doesn’t save much time, although 100 microseconds is already sufficient.
The results are good, but if you look at the frame image, there are still a few allocations being made at the beginning of the broad phase.
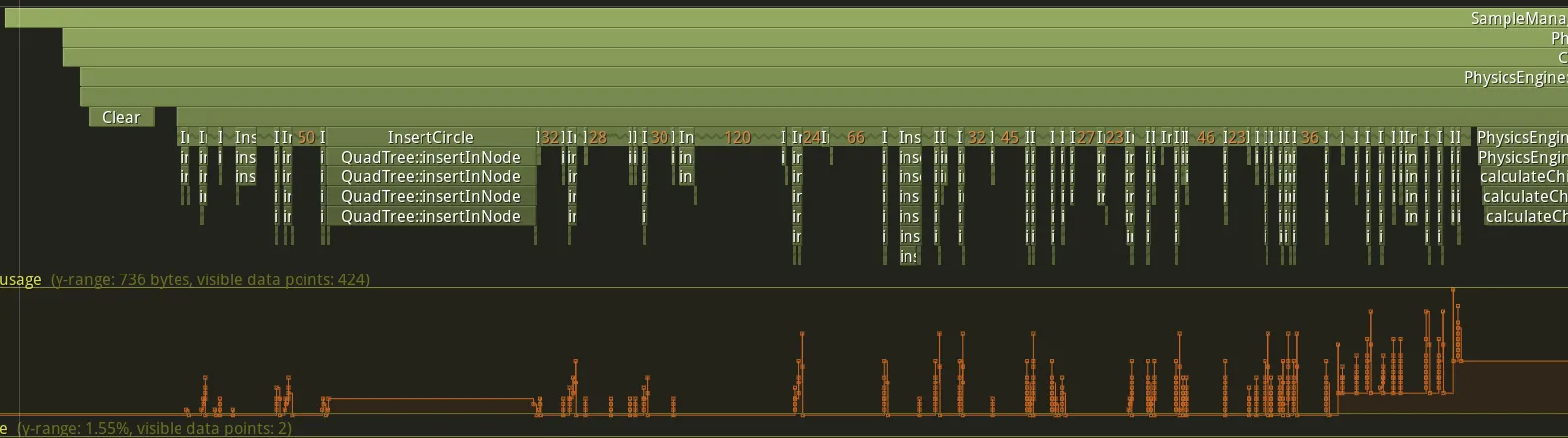
I think that I have a new goal. Let’s try to remove those allocations.
Use of stack memory instead of heap.
Let’s take a look at the “insertInNode” function to see where these allocations are made:
The allocations are made by the vector of remaining colliders.
AllocVector<SimplifiedCollider> remainingColliders{ {_heapAllocator} };
for (const auto& col : node.Colliders)
{
int boundInterestCount = 0;
QuadNode* intersectNode = nullptr;
for (const auto& child : node.Children)
{
if (Math::Intersect(child->Boundary, col.Rectangle))
{
boundInterestCount++;
intersectNode = child;
}
}
if (boundInterestCount == 1)
{
insertInNode(*intersectNode, col.Rectangle, col.ColRef, depth + 1);
}
else
{
remainingColliders.push_back(col);
}
}
node.Colliders.clear();
for (const auto& col : remainingColliders)
{
node.Colliders.push_back(col);
}Because I don’t know how many colliders will have to remain in the parent node, I decided to make a vector to store them. The problem is that a vector dynamically allocates memory and it has a cost. Instead of allocating memory on the heap, let’s try to allocate on the stack. Why not using an array instead of the vector ? I can directly set the size of the array to the max number of colliders (+ 1 for the last collider added) inside a node to make sure you have the right amount of memory, even in the worst-case scenario. It doesn’t matter if you allocate more memory than you need, because it’s taken from the stack. At the end of the function’s scope, this memory will be restored, so let’s make use of it.
Use array instead of vector:
std::array<SimplifiedCollider, QuadNode::MaxColliderNbr + 1> remainingColliders;
// Copy all colliders inside the array.
for (std::size_t i = 0; i < QuadNode::MaxColliderNbr + 1; i++)
{
remainingColliders[i] = node.Colliders[i];
}
node.Colliders.clear();
for (const auto& col : remainingColliders)
{
int boundInterestCount = 0;
QuadNode* intersectNode = nullptr;
for (const auto& child : node.Children)
{
if (Math::Intersect(child->Boundary, col.Rectangle))
{
boundInterestCount++;
intersectNode = child;
}
}
if (boundInterestCount == 1)
{
insertInNode(*intersectNode, col.Rectangle, col.ColRef, depth + 1);
}
else
{
// The collider needs to stay in the parent node.
node.Colliders.push_back(col);
}
}Let’s open Tracy and see if we’ve solved the problem:
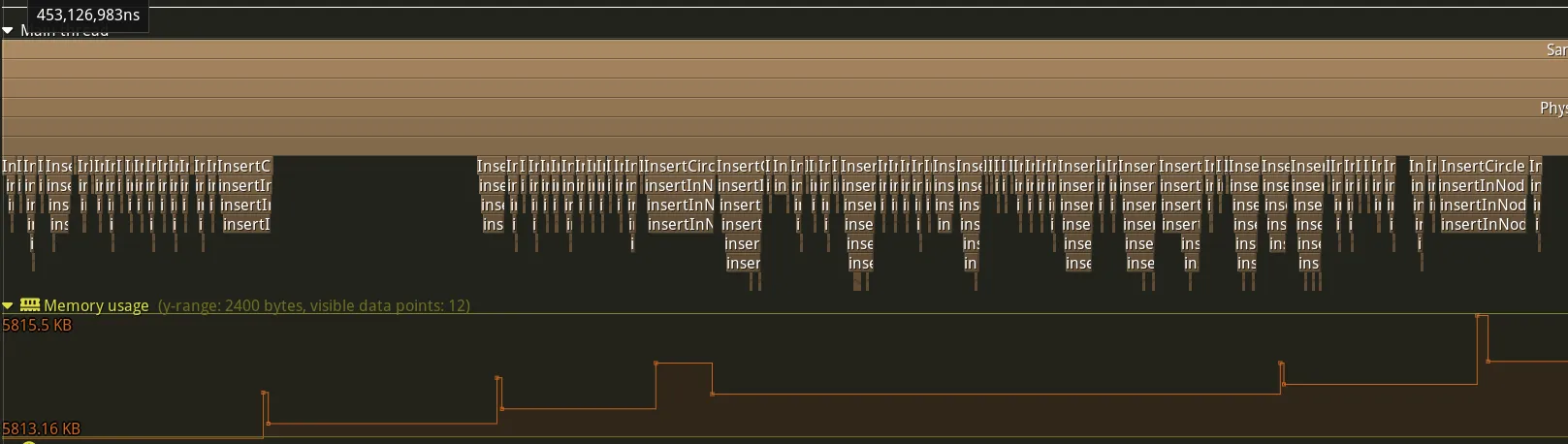
There are still a few allocations, but far fewer than before. The few remaining allocations are due to the fact that the deepest nodes will have a collision vector greater than the maximum number of colliders a node can contain before subdividing. This quantity therefore exceeds that reserved at the start of the program.
Let’s see if this change reduces the execution time of the Insert function:
Note that the values are in nanoseconds because this is a very small function and it is easier to represent the values with a smaller unit in this case.
| Sample (Insert function) | Mean (ns) | Median (ns) | Std dev (ns) | Observations |
|---|---|---|---|---|
| with vector | 149 | 68 | 717 | 200 |
| with array | 117 | 72 | 1039 | 178 |
| [Table: Comparisons of narrow-phase statistics between the non-quad-tree and quad-tree versions.] |
| P(T<=t) two-tail |
|---|
| 2.81e-20 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ns) | Standard error (ns) | Margin of error (ns) | Lower limit (ns) | Greater Limit (ns) |
|---|---|---|---|---|
| 794.3585859 | 78.3347616 | 154.3280979 | 640.030488 | 948.6866837 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
We save between 600 and 950 nanoseconds, which isn’t too bad for a small function like this. It was worth it to remove these allowances. It also makes the code more real time safe.
Final state of the broad phase
I think I’ve really improved my broad phase. Let’s compare the statistics between the first version and the latest one of the “resolveBroadPhase” function:
| resolveBroadPhase | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| First version | 3.37 | 3.31 | 0.494 | 200 |
| Last version | 2.16 | 2.06 | 0.596 | 178 |
| P(T<=t) two-tail |
|---|
| 1.14e-58 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 1.246780332 | 0.04787696109 | 0.09457076147 | 1.152209571 | 1.341351094 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
Overall, I was able to save 1.2ms by better managing memory and allocations in my quad-tree. That’s not too bad for a function that’s called every frame. What’s more, the code is more real time safe this way. I’m satisfied with the result for the broad phase. Now let’s look at what we can do with the narrow phase.
Reduce narrow-phase execution.
Now that the broad phase is fine as it is, let’s take a closer look at the narrow phase:
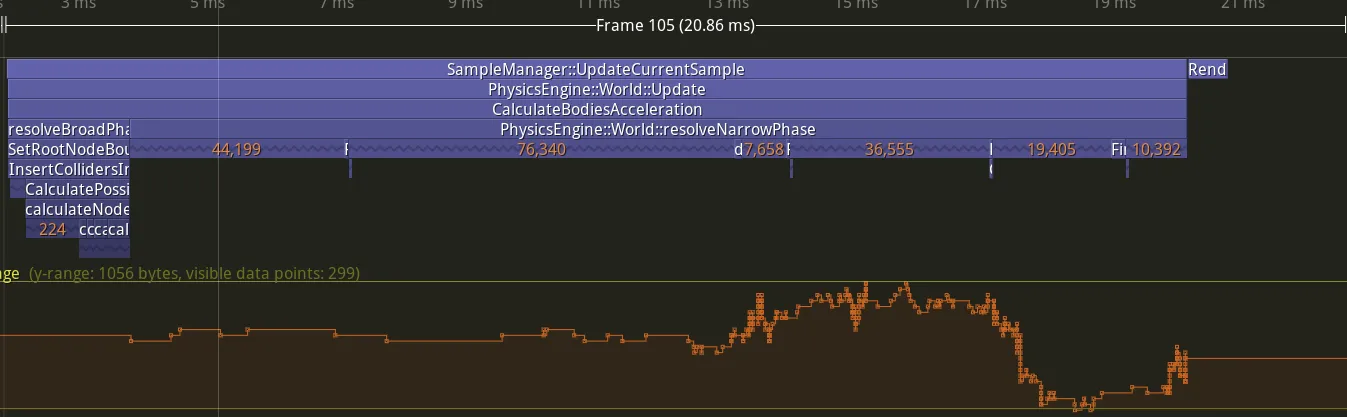
| Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|
| 18.5 | 18.62 | 7.47 | 381 |
| [Table: resolveNarrowPhase function statistics.] |
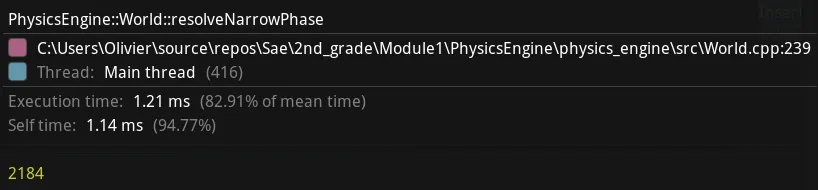
18ms to resolve the narrow phase is really too much. I need to find a way to reduce the time this part of the engine takes. As you can see, the unordered_set does a lot of allocations and deallocations. Is there a cheaper alternative?
Remove unordered_set
Currently, I use an unordered_set to avoid having the same pair twice in my data structure, in addition to the fact that it uses the hash function to quickly find the look-up element.
Current code:
for (auto& possiblePair : possiblePairs)
{
auto& colliderA = GetCollider(possiblePair.ColliderA);
auto& colliderB = GetCollider(possiblePair.ColliderB);
const auto doCollidersIntersect = detectContact(colliderA, colliderB);
#ifdef TRACY_ENABLE
ZoneNamedN(FindPair, "Find pair", true);
#endif
auto it = _colliderPairs.find(possiblePair);
#ifdef TRACY_ENABLE
ZoneNamedN(CheckIfItsANewPair, "Check if it's a new pair", true);
#endif
if (it != _colliderPairs.end())
{
if (!doCollidersIntersect)
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerExit(possiblePair.ColliderA,
possiblePair.ColliderB);
}
#ifdef TRACY_ENABLE
ZoneNamedN(ErasePair, "Erase pair", true);
#endif
_colliderPairs.erase(it);
}
else
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerStay(possiblePair.ColliderA,
possiblePair.ColliderB);
}
}
}
else
{
if (doCollidersIntersect)
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerEnter(possiblePair.ColliderA,
possiblePair.ColliderB);
}
#ifdef TRACY_ENABLE
ZoneNamedN(InsertPair, "Insert pair", true);
#endif
_colliderPairs.insert(possiblePair);
}
}
}But now I generate the collider pairs with my quad-tree. There will never be the same pair twice. So why not use a vector ?
The problem with a vector is knowing which colliders to keep or not in the current pairs. But if I think about it carefully, in each frame, the colliders which overlap are the current new pairs of the world. I just have to store them in a vector then, for each of the pairs that touch each other, I just have to look if I already have this pair or not and activate the TriggerEnter event in this case.
Then I traverse the vector through old pairs and I see if they are part of the new pairs currently in overlap. If this is not the case, I activate the TriggerExit event. Finally I set the value of the old or new pairs at the end of the frame:
New code:
const auto& possiblePairs = _quadTree.PossiblePairs();
#ifdef TRACY_ENABLE
ZoneValue(possiblePairs.size());
#endif
AllocVector<ColliderPair> newPairs{ StandardAllocator<ColliderPair>{_heapAllocator} };
newPairs.reserve(possiblePairs.size());
for (const auto& possiblePair : possiblePairs)
{
auto& colliderA = GetCollider(possiblePair.ColliderA);
auto& colliderB = GetCollider(possiblePair.ColliderB);
if (detectContact(colliderA, colliderB))
{
newPairs.push_back(possiblePair);
}
}
for (const auto& newPair : newPairs)
{
Collider& colliderA = GetCollider(newPair.ColliderA);
Collider& colliderB = GetCollider(newPair.ColliderB);
const auto it = std::find(_colliderPairs.begin(), _colliderPairs.end(), newPair);
// If there was no collision in the previous frame -> OnTriggerEnter.
if (it == _colliderPairs.end())
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerEnter(newPair.ColliderA, newPair.ColliderB);
}
}
// If there was a collision in the previous frame and there is always a collision -> OnTriggerStay.
else
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerStay(newPair.ColliderA, newPair.ColliderB);
}
}
}
for (auto& colliderPair : _colliderPairs)
{
Collider& colliderA = GetCollider(colliderPair.ColliderA);
Collider& colliderB = GetCollider(colliderPair.ColliderB);
const auto it = std::find(newPairs.begin(), newPairs.end(), colliderPair);
// If there is no collision in this frame -> OnTriggerExit.
if (it == newPairs.end())
{
if (colliderA.IsTrigger() || colliderB.IsTrigger())
{
_contactListener->OnTriggerExit(colliderPair.ColliderA,
colliderPair.ColliderB);
}
}
}
_colliderPairs = newPairs;Let’s look at the statistics to see if our change is profitable:
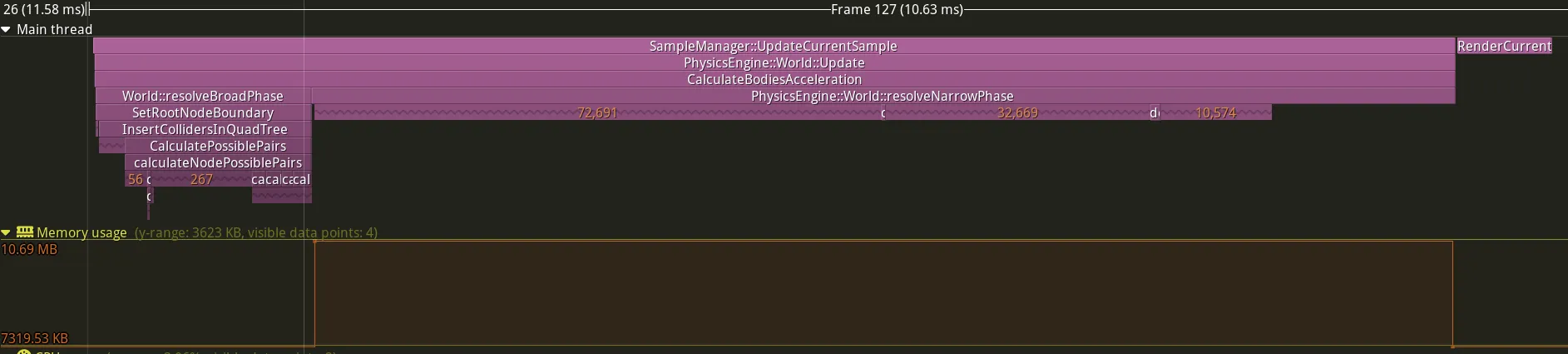
| resolveNarrowPhase | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| First version | 18.5 | 18.62 | 7.47 | 381 |
| Last version | 7.95 | 7.85 | 1.29 | 515 |
| P(T<=t) two-tail |
|---|
| 3.30e-92 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 10.55676636 | 0.38869982 | 0.7641910525 | 9.792575305 | 11.32095741 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
We notice a huge difference in time between the two versions of the narrow phase. Already thanks to the value of the t-test which proves it but above all thanks to the limits of the confidence interval which shows the time saving of around 10ms.
This proves that the unordered_set allocations were not the most optimal. On the other hand, what resets long is the search for peers in the vector of current pairs. Let’s see if we can reduce the number of pairs to search for.
Reduce the number of pairs to find.
To find an element in a data structure such as the vector, you have to go through the elements from the beginning until you find the element in question. If our vector contains a lot of elements, it will take a long time to do a std::find on it. In fact, the longer the vector, the less chance there is of having the value stored in one of the caches. Otherwise it means a lot of cache miss so is slow access to the value.
I used tracy’s “ZoneValue” option to display the size of my possible pair vector coming out of the quad-tree:
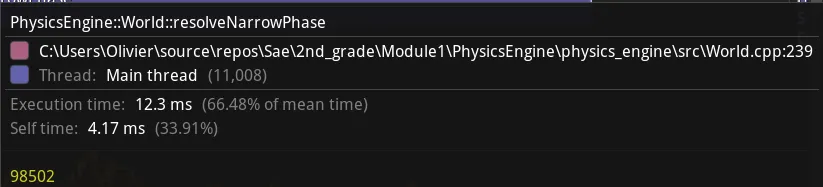
I need to find a way to filter out pairs that really have overlap potential in the quad-tree.
Currently the quad-tree works as follows:
The colliders of the parent nodes are compared with all the colliders of the child nodes. However, most of these comparisons are useless because the collider in question can be very far from the colliders of child nodes. Maybe it’s easier to understand with a diagram:
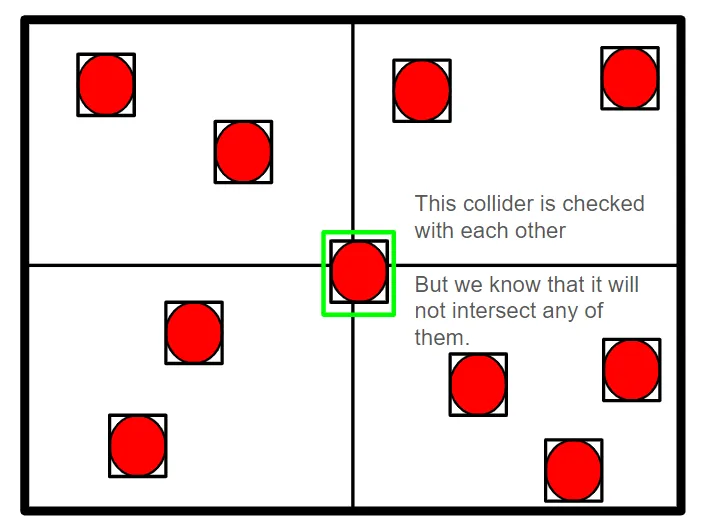
So to avoid creating useless pairs, I can only interest the pair of colliders which have their simplified shape which overlaps. This way we avoid a large number of unnecessary comparisons and can reduce my memory accesses:
QuadTree.cpp -> calculateNodePossiblePairs()
// begin of calculateNodePossiblePairs function.
for (std::size_t i = 0; i < node.Colliders.size(); i++)
{
auto& simplColA = node.Colliders[i];
for (std::size_t j = i + 1; j < node.Colliders.size(); j++)
{
auto& simplColB = node.Colliders[j];
if (Math::Intersect(simplColA.Rectangle, simplColB.Rectangle))
{
_possiblePairs.push_back(ColliderPair{ simplColA.ColRef, simplColB.ColRef });
}
}
// rest of calculateNodePossiblePairs function.
}
...
// begin of calculateChildrenNodePossiblePairs function.
// For each colliders in the current node, compare it with the simplified collider from its parent node.
for (const auto& nodeSimplCol : node.Colliders)
{
if (Math::Intersect(simplCol.Rectangle, nodeSimplCol.Rectangle))
{
_possiblePairs.push_back(ColliderPair{ simplCol.ColRef, nodeSimplCol.ColRef });
}
// rest of calculateChildrenNodePossiblePairs function.
}Let’s look at how many possible pairs are generated now:
Oh wow, this significantly reduces memory accesses. It’s time to do the statistical tests to see how much time this saves us:
| resolveNarrowPhase | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| previous version | 7.95 | 7.85 | 1.29 | 515 |
| new version | 1.45 | 1.27 | 0.506 | 1291 |
| P(T<=t) two-tail |
|---|
| 0 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 6,488111856 | 0.05908054316 | 0.1160378747 | 6.372073981 | 6.60414973 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
The t-test returns the value 0. That says it all. There is no way that the previous version would be faster than the current one. The time saving is estimated at around 6.45ms with a very small margin of error. We have therefore indeed shortened the time taken by the narrow phase.
Final state of the narrow phase.
We have greatly improved the execution speed of the narrow phase. Let’s analyze the statistical differences between the first implementation of the narrow phase and the last.
| resolveNarrowPhase | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| First version | 18.5 | 18.62 | 7.47 | 381 |
| Last version | 1.45 | 1.27 | 0.506 | 1291 |
| P(T<=t) two-tail |
|---|
| 1.08e-150 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 17.02925156 | 0.3861128878 | 0.7592111286 | 16.27004043 | 17.78846269 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
We can see that the narrow phase has been greatly improved. By choosing a less expensive data structure and having optimized the number of memory accesses, we were able to reduce the duration of the narrow phase by 16ms.
Conclusion
Let’s compare the state of the program before and after the optimizations applied to it:
 
GIFs are at 30 fps, so it’s hard to tell whether the right-hand version is actually fluid. So let’s have a look at some frame images from Tracy:


Let’s take a look at the time saved when executing the world’s “Update” function:
| world Update | Mean (ms) | Median (ms) | Std dev (ms) | Observations |
|---|---|---|---|---|
| without optimizations | 792.32 | 828.95 | 157.16 | 16 |
| with optimizations | 2.64 | 2.44 | 0.622 | 1291 |
| P(T<=t) two-tail |
|---|
| 1.20e-23 |
| [Table: Student T-Test Values using P = 5%.] |
| Mean Difference (ms) | Standard error (ms) | Margin of error (ms) | Lower limit (ms) | Greater Limit (ms) |
|---|---|---|---|---|
| 808.3191733 | 23.20918389 | 47.70716026 | 760.612013 | 856.0263335 |
| [Table: Difference of means and confidance interval (confidence level 95%) [lower limit ; greater limit]] |
With all the changes made to my engine I saved between 760ms and 856ms. I’m satisfied with the result. The main factors making my program slow were memory allocations and accesses. I was able to save a lot of time on my frames by allocating as much memory as possible at the start of the program to avoid allocating as much as possible during the update. I was also able to save a lot of time by doing a bigger sort on the colldier pairs I was generating, which shortened the time spent searching for data in memory. As a result, my code is more real time safe and, above all, much faster to execute.
Well, I think I’ve talked enough
Thank you very much for taking the time to read my blog post. Here’s the source code of my project if you’re curious: https://github.com/Chocolive24/PhysicsEngine
You can also check out my game projects on my itch.io page: https://itch.io/profile/chocolive
Pachoud Olivier - Games Programmer student at Sae Institute Geneva